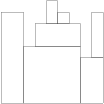
StoneWall solution

Task

The task is to find a minimum number of rectangles that fulfil a criteria:

You are going to build a stone wall. The wall should be straight and N meters long, and its thickness should be constant; however, it should have different heights in different places. The height of the wall is specified by an array H of N positive integers. H[I] is the height of the wall from I to I+1 meters to the right of its left end. In particular, H[0] is the height of the wall’s left end and H[N−1] is the height of the wall’s right end.

The wall should be built of cuboid stone blocks (that is, all sides of such blocks are rectangular). Your task is to compute the minimum number of blocks needed to build the wall.

Write a function: int solution(vector<int> &H);

that, given an array H of N positive integers specifying the height of the wall, returns the minimum number of blocks needed to build it.

For example, given array H containing N = 9 integers:
H[0] = 8 H[1] = 8 H[2] = 5 H[3] = 7 H[4] = 9 H[5] = 8 H[6] = 7 H[7] = 4 H[8] = 8

the function should return 7. The figure shows one possible arrangement of seven blocks.

Write an efficient algorithm for the following assumptions:

N is an integer within the range [1..100,000];

each element of array H is an integer within the range [1..1,000,000,000].

Solution 1

The simplest way to build a wall would be to have N blocks, each the height of the wall. You can use one block for two columns if and only if the columns are the same height and have no shorter columns between them.

Therefore this task amounts to counting the number of such columns.

This shows a simple implementation of this:


int solution(vector<int> &H) {

  int numEqual = 0;
  for (size_t i = 0; i < H.size(); i++) {
    int height = H[i];

    for (size_t j = i + 1; j < H.size(); j++) {
      int next = H[j];

      if (next == height) {
        numEqual++;
        break;
      }

      if (next < height) {
        break;
      }
    }
  }
  return  H.size() – numEqual;
}

While this passes the correctness, codility gives it a performance score of 77%.

Now, if H is populated with random data then there is a 50% chance the next column is shorter than the current, so the average time the inner loop executes will be <2 regardless of N.

This means this function is O(N) on average-case and best-case data.

However, the worst-case data is where the columns always increase in height, so the inner loop executes up to N. This has a time complexity of O(N²).

It fails because it is timed with the worst-case data.

This is where Codility’s sloppy use of the word ‘efficiency’ becomes a problem; the solution that passes their test (below) is actually slower in the average case.

Results

Correctness	100%
Performance	77%
Time Complexity	O(N) (average)

Solution 2

In order to reduce the worst-case time, we have to find a way of reducing the number of columns to compare the current one to.

Firstly, we can look backwards rather than forwards and keep a list of columns found so far, then we can remove ones from the list if they cannot be paired up with any later columns.

For example, consider this sequence:

When we process column e, we can discard column d – no later columns can be paired with it because e is shorter. In fact we can remove all the columns from our list that are shorter or the same height as e, till we are left with just a and e.

This means that our list will contain columns in strictly increasing order, which in turn means we can stop processing it as soon as we reach a column shorter than the current one; all remaining columns will also be shorter.

A stack is the ideal data structure to store a list which is only accessed by adding or removing from the end. So that gives us the following algorithm:


#include <stack>
int solution(vector<int> &H) {

  // list of previous column sizes smaller than current
  stack<int> prevSmaller;
  int numEqual = 0;
  for (size_t i = 0; i < H.size(); i++) {
    int height = H[i];
    while (prevSmaller.size() > 0) {
      int prev = prevSmaller.top();

      if (prev == height) {
        numEqual++;
        prevSmaller.pop();
        break;
      } else {
        if (prev > height) {
          prevSmaller.pop();
        } else {
          break;
        }
      }
    }
    prevSmaller.push(height);
  }
  return H.size() – numEqual;
}

This is O(N) for best-case, average and worst-case data.

Results

Correctness	100%
Performance	100%
Time Complexity	O(N)

Test Function

This code tests the solution


int main() {
  vector<int> A9{8, 8, 5, 7, 9, 8, 7, 4, 8};
  assert(solution(A9) == 7);

  vector<int> A2{1000000000, 7, 6, 5, 4, 3, 2, 1};
  assert(solution(A2) == 8);
  vector<int> A3(100000, 1);
  assert(solution(A3) == 1);
  vector<int> A4(100000, 1000000000);
  assert(solution(A4) == 1);
}

StoneWall solution

Task

Solution 1

Results

Solution 2

Results

Test Function

Index of solutions to Codility Lessons

Leave a Reply Cancel reply