Categories
coding solutions

NumberOfDiscIntersections O(N) Solution

NumberOfDiscIntersections O(N) solution

Task

We draw N discs on a plane. The discs are numbered from 0 to N − 1. An array A of N non-negative integers, specifying the radiuses of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].

We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).

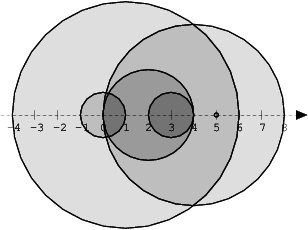
The figure below shows discs drawn for N = 6 and A as follows:

A[0] = 1 A[1] = 5 A[2] = 2 A[3] = 1 A[4] = 4 A[5] = 0

There are eleven (unordered) pairs of discs that intersect, namely:
  • discs 1 and 4 intersect, and both intersect with all the other discs;
  • disc 2 also intersects with discs 0 and 3.

Write a function: int solution(vector<int> &A);

that, given an array A describing N discs as explained above, returns the number of (unordered) pairs of intersecting discs. The function should return −1 if the number of intersecting pairs exceeds 10,000,000.

Write an efficient algorithm for the following assumptions:
  • N is an integer within the range [0..100,000];
  • each element of array A is an integer within the range [0..2,147,483,647].

Solution 1

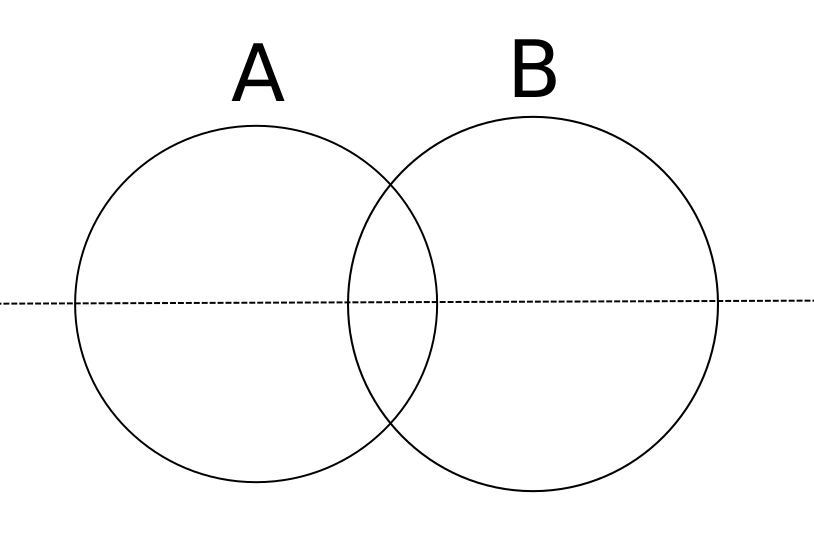
If two discs A and B, where A is to the left of B, overlap then the right hand edge of A is at the same point or to the right of the left hand edge of B.
This suggests the following algorithm:
Create a list of the left hand edges. Create a list of the right hand edges. for each left hand edge (lh) overlap := number of right hand (rh) edges >= lh edge count += overlap
There are a couple of flaws in the above algorithm, viz:
  • It counts a disc as overlapping itself
  • It counts discs as overlapping where A is to the right of B, and the rh of A is therefore to the right of the lh of B
Fortunately it is easy to calculate how many intersections are wrongly counted like this, and correct for them.
For A[0], it wrongly counts N items (itself and the following N-1 discs to the right), for A[1] it adds N-1 items, etc.
This means the additional intersections counted are: N + (N-1) + … +1 = N(N+1)/2
The above algorithm can be optimised by using sorted lists, like this:
lhes:= a sorted list of the left hand edges rhes:= a sorted list of the right hand edges rhindex := 0 count:= 0 for lhs = each left hand edge, from smallest to largest while (rhes[rhindex++] < lhs); // note final rh edge has to be >= last lh edge, so this will always terminate rhEdgesCount := rhes.size – rhindex count += rhEdgesCount return (count – N(N+1)/2)
The following implements this. Note, we have to subtract the adjustment before the loop, so we can break out early if count > 10,000,000
  1.  
  2. #include <algorithm>
  3. #include <cassert>
  4. #include <vector>
  5.  
  6. int solution(vector<int> &A) {
  7. const int MAX_COUNT = 10000000;
  8. // create sorted arrays of left-hand edges, and rh edges
  9. vector<int64_t> lhes;
  10. vector<int64_t> rhes;
  11. ulong N = A.size();
  12. for (size_t i = 0; i < N; i++) {
  13. // for all prev discs – is rhs intersecting with lhs?
  14. long lhs = static_cast<long>(i) – A[i];
  15. lhes.push_back(lhs);
  16. long rhs = A[i] + static_cast<long>(i);
  17. rhes.push_back(rhs);
  18. }
  19.  
  20. std::sort(lhes.begin(), lhes.end());
  21. std::sort(rhes.begin(), rhes.end());
  22.  
  23. long count = 0;
  24. // now we remove ones where circle centre is to right or same pos. of circle. all of these will be counted in the loop
  25. // below sum = n(n+1)/2. note includes each item as intersecting itself, so is N + (N-1) + …
  26. count -= (N + 1) * N / 2;
  27. size_t rhIndex = 0;
  28.  
  29. // for each lh edge, count number of rh edges >= it
  30. for (size_t i = 0; i < lhes.size(); i++) {
  31. int64_t lhs = lhes[i];
  32. while (rhes[rhIndex] < lhs)
  33. rhIndex++;
  34. if (rhIndex == rhes.size())
  35. break;
  36. // add all circles where rh edge >= current left hand edge
  37. count += rhes.size() – rhIndex;
  38. if (count > MAX_COUNT)
  39. return -1;
  40. }
  41. assert(count <= MAX_COUNT);
  42. return static_cast<int>(count);
  43. }

Results

This scores 100% on codility for both correctness and performance. The complexity is O(N * log(N)) and is dominated by the sorting.
Correctness100%
Performance100%
Complexity O(N * log(N))

Solution 2

However, I was not happy with the above, the inner loop (lines 32-37) seems a bit messy.
So I googled for other solutions and found this: stackoverflow.com/a/16814894 by user Толя.
While this uses a different algorithm than the above, it has a neat hack:

For right hand edges that are >=N it is not necessary to store the exact value, only that they are >=N (because it is not possible for a lh edge to be >=N).

This means the rh sides can be stored in an array [0..N-1], with the elements of the array having a count of the number of edges at that point.

The same can be done with the lh edges.
Applying this to the above, we don’t need to sort the arrays, and the count of rh edges can be calculated by counting down the array keeping a running total.
This gives us this algorithm:
clear lhcount, rhcount For radius in A lhe := max(0,centre – radius) lhcount[lhe]++ rhe:= min(N-1,centre+radius) rhcount[rhe]++ count := 0 rhSum := 0 for i := N-1 downto 0 rhSum += rhcount[i] count += lhcount[i] * rhsum return (count – N(N+1)/2)
The implementation is below
  1.  
  2. #include <cassert>
  3. int solution(vector<int> &A) {
  4. const int MAX_COUNT = 10000000;
  5. ulong N = A.size();
  6. // create arrays of frequency of left-hand edges, and rh edges
  7. vector<int> lhes(N,0);
  8. vector<int> rhes(N,0);
  9. for (size_t i = 0; i < N; i++) {
  10. // for all discs – count instances of edges at points
  11. ulong lhs = static_cast<ulong>(max(0, static_cast<int>(i) – A[i]));
  12. lhes[lhs]++;
  13. ulong rhs = min(N – 1, static_cast<ulong>(A[i]) + i);
  14. rhes[rhs]++;
  15. }
  16. long count = 0;
  17. // now we remove ones where circle center is to right or same pos. of circle. all of these will be counted by loop
  18. // below sum = n(n+1)/2. note includes 0 and N so N + (N-1) + …
  19. count -= (N + 1) * N / 2;
  20. ulong rhSum = 0;
  21. for (long i = N – 1; i >= 0; i–) {
  22. // for all prev discs – is rhs intersecting with lhs?
  23. rhSum += rhes[i];
  24. count += lhes[i] * rhSum;
  25. if (count > MAX_COUNT)
  26. return -1;
  27. }
  28.  
  29. assert(count <= MAX_COUNT);
  30. return static_cast<int>(count);
  31. }

Results

This scores 100% on codility for both correctness and performance. The time complexity is O(N).
Correctness100%
Performance100%
ComplexityO(N)

Other Solutions

The only other O(N) solutions I found are variations of the one by Толя.
This works as follows:
  • Firstly, build arrays of the number of lh edges and rh edges at each position 0..N-1, as above
  • Then iterate from 0..N-1, using these arrays to keep track of how many discs are overlapping at the current point.
  • For each lh edge, add on the number of overlapping discs to the count
  • If there are > 1 lh edges at a point, we also need to add on the number of new overlaps caused by these new discs overlapping each other. For r new discs this is r(r-1)/2 (the number of combinations of 2 items out of r).
This is my implementation in C++:
  1.  
  2. #include <cassert>
  3. int solution(vector<int> &A) {
  4. const int MAX_COUNT = 10000000;
  5. size_t N = A.size();
  6. // create arrays of frequency of left-hand edges, and rh edges
  7. vector<int> lhes(N,0);
  8. vector<int> rhes(N,0);
  9. for (size_t i = 0; i < N; i++) {
  10. // for all discs – count instances of edges at points
  11. int lhs = max(0, static_cast<int>(i) – A[i]);
  12. lhes[lhs]++;
  13. int rhs = min(N – 1, static_cast<int>(A[i]) + i);
  14. rhes[rhs]++;
  15. }
  16. int count = 0;
  17. int overlapping = 0;
  18. for (size_t i = 0; i < N; i++) {
  19. // find number of new discs at this point
  20. int newDiscs = lhes[i];
  21. count += newDiscs * overlapping;
  22. count += newDiscs * (newDiscs – 1) / 2;
  23. if (count > MAX_COUNT)
  24. return -1;
  25. // update with number of new discs, minus number now passed
  26. overlapping += newDiscs – rhes[i];
  27. }
  28. assert(count <= MAX_COUNT);
  29. return count;
  30. }
Results

Codility Results
Correctness100%
Performance100%
ComplexityO(N)
These blogs also have some variation of Толя’s algorithm
These blogs have a solution that involves sorting lists of edges (as in solution 1) and then iterating through, counting overlaps (as in Толя’s algorithm)

Test Function

This code tests the solution

  1.  
  2. int main() {
  3. vector<int> A9(100000, 0);
  4. assert(solution(A9) == 0);
  5.  
  6. vector<int> A2{};
  7. assert(solution(A2) == 0);
  8.  
  9. vector<int> A1{1, 5};
  10. assert(solution(A1) == 1);
  11.  
  12. vector<int> A7{1, 5, 2, 1};
  13. assert(solution(A7) == 5);
  14.  
  15. vector<int> A6{1, 5, 2};
  16. assert(solution(A6) == 3);
  17.  
  18. vector<int> A{1, 5, 2, 1, 4, 0};
  19. assert(solution(A) == 11);
  20.  
  21. vector<int> A3{1, 5, 2, 1, 4, 0, 0};
  22. assert(solution(A3) == 13);
  23. vector<int> A4{1, 5, 2, 1, 4, 0, 0, 0};
  24. assert(solution(A4) == 14);
  25. vector<int> A5{1, 5, 2, 1, 4, 0, 0, 0, 0};
  26. assert(solution(A5) == 15);
  27.  
  28. vector<int> A8{1, 2147483647, 0};
  29. assert(solution(A8) == 2);
  30. }

Index of solutions to Codility Lessons

Leave a Reply

Your email address will not be published. Required fields are marked *